최근에 알고리즘 스터디에서 DFS를 공부하면서, 예전에 정리했던 순열과 조합에 대한 포스팅을 보고 역시 제대로 공부할 때가 많이 다르다는 것을 깨닫고 쓰는 포스팅입니다...🥹
📌 중복 순열 구현하기
중복 순열은 만약 봉투안에 구슬 5개가 있을 때, 매번 5개 중 1개를 뽑는 예시를 들 수 있습니다. 그리고 추가적으로 각각 다른 순서도 다른 상황임을 가정합니다.
예를 들어, [1,2,3,5,5]를 뽑은 상황과 [5,5,1,2,3]은 다른 상황으로 가정합니다.
- Q. 숫자구슬 5개를 순서대로 뽑는 경우의 수를 구해주세요. (중복 허용)
function solution(bead) {
let answer = [];
let tmp = Array.from({length: bead.length}, () => 0); // 뽑은 구슬 담는 곳
function DFS(L) {
if(L === bead.length) answer.push(tmp.slice());
else {
for(let i = 0; i < bead.length; i++){
tmp[L] = bead[i];
DFS(L+1);
}
}
}
DFS(0);
return answer.length;
}
solution([1,2,3,4,5]); // 5 * 5 * 5 * 5 * 5 📌 순열 구현하기
위와 같은 문제로 순열을 구현합니다.
순열은 위의 중복순열과 다르게 순서는 존재하지만, 중복은 허용하지 않습니다.
예를 들어, [1,2,3,5,5] 이런 경우는 허용되지 않습니다.
또한 [1,2,3,4,5], [5,4,3,2,1]은 다른 경우로 판단합니다.
function solution(bead) {
let answer = [];
let n = bead.length;
let tmp = Array.from({length: n}, () => 0); // 뽑은 구슬 담는 곳
let check = Array.from({length: n}, () => 0); // 구슬을 뽑았는지 체크하는 곳
function DFS(L) {
if(L === n) answer.push(tmp.slice());
else {
for(let i = 0; i < n; i++){
// 구슬이 뽑힌 구슬이 아니라면
if(check[i] === 0){
check[i] = 1; // 구슬을 뽑았다고 표시한다.
tmp[L] = bead[i];
DFS(L+1);
check[i] = 0; // 재귀를 나올 때, 구슬을 뽑지 않았다고 수정해준다.
}
}
}
}
DFS(0);
return answer.length; // 5 * 4 * 3 * 2 * 1
}
solution([1,2,3,4,5]); // 📌 조합 구현하기
그렇다면 5개의 구슬 중에서 3개를 고르는 조합은 어떻게 구할까요?
예를들어, 조합은 이 둘의 상황은 동일하다고 판단합니다.
[1,2,5]을 뽑은 경우, [5,2,1]를 뽑은 경우는 같은 경우입니다.
function solution(bead, n) {
let answer = [];
let tmp = Array.from({length: n}, () => 0);
function DFS(L, s){
if(L === n) answer.push(tmp.slice());
else {
for(let i = s; i < bead.length; i++){
tmp[L] = bead[i];
DFS(L+1, i+1);
}
}
}
DFS(0,0);
return answer;
}
solution([1,2,3,4,5], 3) // 5C3 => 10개이외에도 DFS같은 경우에는 브레이크 포인트를 잘 잡아주는게 가장 큰 핵심이겠구나! 생각이 들었던 것 같아요.
확실히 정리하니까 너무 좋네요🥹 추가적으로 이진트리 DFS같은 경우에는 뽑았을 경우, 뽑지 않았을 경우로 DFS를 넘기는 수순이라고 생각하면 됩니다!
📌 번외 조합 구현하기
조합은 익히 알고 있듯이 아래와 같은 방식으로 계산될 수 있는데요,
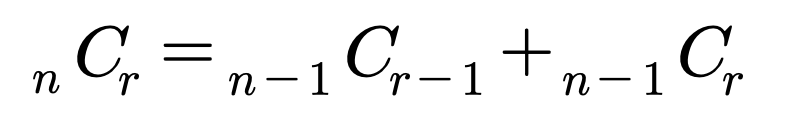
이 조합 계산식을 재귀로 구현하면 어떨까요?
function solution(n, r) {
let answer;
let dy = Array.from(Array(35), () => Array(35).fill(0));
function DFS(n, r) {
if(dy[n][r] > 0) return dy[n][r];
if(n === r || r === 0) return 1;
else return dy[n][r] = DFS(n-1, r-1) + DFS(n-1, r);
}
answer = DFS(n,r);
return answer;
}
solution(5,3) // 10
